| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 이펙티브 자바
- dfs
- 세그먼트 트리
- ddd
- 데이터 flow
- series
- equals
- 알고리즘
- 파이썬
- Redis
- BFS
- 스프링
- JPA
- spring security
- springboot
- 위상정렬
- java
- DP
- 다익스트라
- docker
- 자바
- disjoint set
- dataframe
- pandas
- 비트마스크
- UML
- 헥사고날 아키텍처
- 문자열
- 포트앤어댑터 아키텍처
- 백준
- Today
- Total
코딩못하는사람
세그먼트 트리(2042 구간 합 구하기) 본문
세그먼트 트리란?
세그먼트 트리(Segment Tree) 또는 인덱스 트리(Index Tree)는 다음 두 연산을 어떻게 더 효율적으로 할까에 대한 고민에서 출발한다.
-
구간 l, r (l ≤ r)이 주어졌을 때, A[l] + A[l+1] + ... + A[r-1] + A[r]을 구해서 출력하기
-
i번째 수를 v로 바꾸기. A[i] = v
두번째 연산은 O(1)에 해결할 수 있겠지만 첫 번째 연산은 l-r의 길이만큼의 시간 O(NM)이 쿼리가 요청될 때 마다 소요될 것이다. (쿼리 m번 구간크기 n)
따라서 우리는 M과 N이 클때를 위한 자료구조인 세그먼트 트리를 알아야한다.
가장 기본적인 2,3,7,4,5,9,6,1의 구간합을 구하는 세그먼트 트리를 보자.
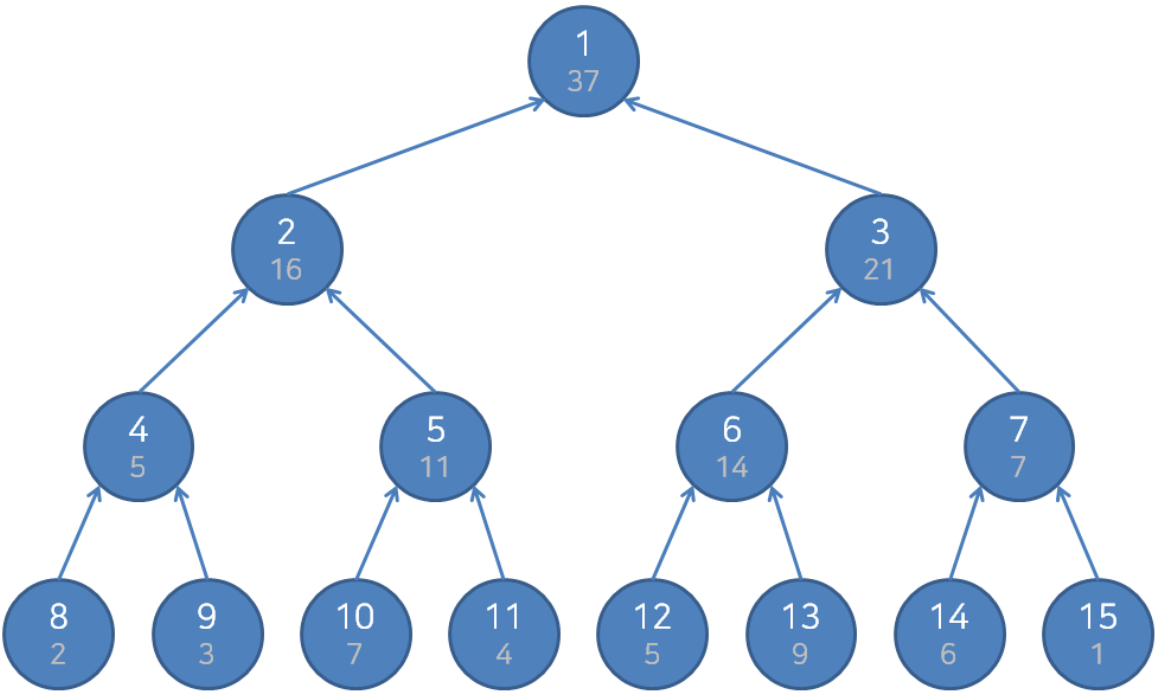
트리는 완전 이진 트리로 구성된다. 또한 트리의 특성상 자식 노드는 부모노드*2, 부모노드*2+1인 특징을 살리기위해 루트노드를 1로 설정한다. 다음과 같이 배열의 수를 트리의 맨 밑에 순서대로 넣고 자식 노드들의 합을 부모노드로 올려준다면 구간합을 쉽게 구할 수 있다.
예를 들어 2번 부터 5번까지의 부분합을 구한다고 생각해보자.

전체 구간을 쪼개서 2~5라는 구간을 나눠서 찾아야 한다. 전체 배열의 크기는 1번에서 8번까지 있으므로 1~4,5~8로 맨처음 쪼갤 수 있을 것이다. 또 1~4를 1~2,3~4 그 다음은 1~2를 1,2로 나누어서
결국 2~5구간합 은 2,3~4,5의 노드의 값들로 이루어진 것을 확인 할 수 있다.
O(N)의 시간이 O(logN)의 시간으로 줄어든다.
원소의 값을 수정하기
값이 수정되는 쿼리가 들어오기도 한다. 하나의 원소가 변경되면 트리 곳곳의 값이 바뀌게 된다.
하지만 바뀐 곳의 부모노드를 타고 올라가 루트 노드까지만 변경될 것이므로 변경된 값 만큼을
부모노드를 타고 올라가면서 더해주면 된다.
어떻게 구현할까?
세그먼트 트리의 구현은 3단계이다.
- 트리의 크기 선언 후 DP로 구간합 전처리하기
- 구간합을 구하는 sum함수 선언
- 원소를 수정하는 update함수 선언
1단계.
트리의 형태가 완전 이진트리이므로 최대 들어올 수 있는 원소의 갯수를 N이라고 가정했을때
트리의 크기는 최대 2*2^ceil(log2(N))가 된다.(ceil은 올림처리,여기부터 2^ceil(log2(N))=size라고 지칭)
예를들어 들어오는 원소가 7개라면 16이라는 뜻인대 위의 그림처럼 루트노드부터
리프노드 전까지 7개, size크기인 리프노드들 8개가 된다. 트리의 배열을 size*2로 선언해준다.
이제 리프노드에 들어오는 값들을 트리에 넣어주면 된다.리프노드는 인덱스가 size부터 시작일 것이다.
그후 size-1의 인덱스들부터 루트 노드까지는 자식노드들의 합으로 DP를 이용해서 채워준다.
2단계.
트리는 완성되었으므로 원하는 구간이 주어질 때 구간을 찾아가서 합을 꺼내오는 sum 함수를 구현한다.
이분탐색과 같은 원리이다. 전체 구간의 시작점 start 끝점 end를 mid로 계속 나누면서 찾아간다. 내가 원하는 구간이 포함되어있다면 return 해주고 아니라면 버리는 구조이다. 코드를 보면 이해할 것이다.
3단계.
원소를 바꿔준다는 것은 리프노드의 값을 바꿔준다는 것이다. 리프노드의 값을 바꿔주면? 자동적으로 그에 연관된 노드들의 값도 바뀌어야 한다. 바뀌는 곳의 인덱스(size+바뀌는곳-1)에 들어가서 그 노드부터 루트노드까지 타고 올라가서 원래의 값과의 차이인 diff를 모든 노드에 더해준다.
배운점
세그먼트 트리는 내가 어떤 값을 원하느냐에 따라서 다양하게 사용할 수 있다. 가장 기본적인 구간합을 구하는 세그먼트 트리를 구현했지만 조금만 다르게 구현하면 최솟값, 최댓값도 구할 수 있고 구간곱 등도 간단하게 구현할 수 있다.
2042 구간 합 구하기
2042번: 구간 합 구하기
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 합을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄
www.acmicpc.net
접근
N의크기가 백만이고 M과 K가 각각 만까지 가능하다. 따라서 N^2의 시간으로는 시간초과이다.
따라서 NlogN의 시간이 소요되는 세그먼트 트리를 이용해서 간단하게 풀 수 있다.
'알고리즘 정리' 카테고리의 다른 글
| Closest Pair 최근접 점쌍 (2261 가장 가까운 두 점 ) (0) | 2020.11.12 |
|---|---|
| lazy propagation(16975 수열과 쿼리 21) (0) | 2020.11.10 |
| 위상정렬 (Topological Sort),2252 줄세우기 (0) | 2020.09.27 |
| 자료구조 트라이( 백준 5052 전화번호 목록) (1) | 2020.09.18 |
| KMP 알고리즘(문자열 찾기) (1) | 2020.09.11 |



